How to solve sudoku puzzles @ paulspages.co.uk

How to solve sudoku puzzles

Solving sudoku puzzles is easier than it looks, and all but the very hardest puzzles can be solved using just a few simple techniques. You don't need any maths, and you don't need to guess. It's all done by observation and logic, and the most important thing is to stay 100% accurate at all times.

This page covers techniques that will solve most puzzles up to (and including) 'fiendish' or 'very hard' rating.

If you've arrived here direct from a search engine, you may like to try sudoku@paulspages.co.uk - it's a web page that creates puzzles, lets you solve them on screen (or print them out) and will even show you the answer!

Click here for a printer-friendly version of this page.

For an expanded version of this guide, including more extreme solving methods, see SudokuXP's Solving Guide.

1. The Rules.
2. Getting started.
3. Pencilling-in.
4. Serious solving!
5. Extreme puzzles.
6. Quick solving checklist.

1. The Rules.

Here's a 'classical' sudoku puzzle. It's a grid 9 squares wide and 9 squares deep. The lines of squares running horizontally are called rows, and the lines running vertically are called columns. The grid is further divided by the darker lines into nine 3 X 3 square 'boxes'.

Some of the squares already have numbers in them. Your task is to fill in the blank squares. There's only one rule:

Each row, column and box must end up containing all of the numbers from 1 to 9.

This rule has an important side-effect, which is the basis of all solving techniques:

Each number can only appear once in a row, column or box.

2. Getting started.

Solving sudoku is all about eliminating the impossible. It's also about looking at the same thing in different ways.

◊ The crosshatching and slicing/dicing techniques shown in the first part of this page are enough, on their own, to solve most easy puzzles. If you're new to sudoku, it's worth generating some easy puzzles and practising these techniques.

To solve more difficult puzzles you need to use crosshatching in combination with other techniques. These are described in the second part of this page.

Crosshatching - finding squares for numbers.
The obvious way to solve a sudoku puzzle is to find the right numbers to go in the squares. However the best way to start is the other way round - finding the right squares to hold the numbers.

This uses a technique called 'crosshatching', which only takes a couple of minutes to learn. It can solve many 'easy' rated puzzles on its own.

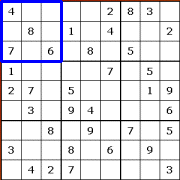
Crosshatching works in boxes (the 3 X 3 square subdivisions of the grid). Look at the top-left box of our sample puzzle (outlined in blue). It has five empty squares. All the numbers from 1 to 9 must appear in the box, so the missing numbers are 1,2,3,5 and 9.

We'll ignore 1 for a moment (because it doesn't provided a good example!), and see if we can work out which square the missing 2 will go into.

To do this, we'll use the fact that a number can only appear once in any row or column. We start by looking across the rows that run through this box, to see if any of them already contain a 2. Here's the result:

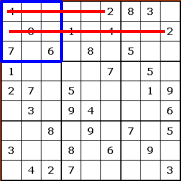
Bingo! The first two rows already contain 2s, which means that squares in those rows can't possibly contain the 2 for this box. That's all we need to know, because the third row only has one empty square, so that must be the home for the 2.

Now let's see if we can place the 3 for this box. This time we end up checking the columns that run down through the box, as well as the rows that run across it:

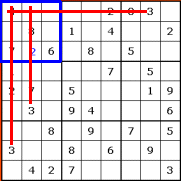
Again, we get a result first time - there's only one empty square that the 3 can possibly go into. You can see from this example why it's called 'crosshatching' - the lines from rows and columns outside the square criss-cross each other.

Of course you don't always get a result first time. Here's what happens when we try to place the 5:

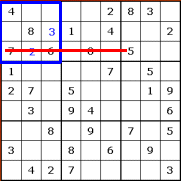
There's only one 5 already in the rows and columns that run through this box. That leaves three empty squares as possible homes for the 5. For the time being, this box's 5 (and its 1 and 9) have to remain unsolved.

Now we move on to the next box:

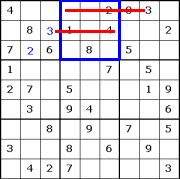
Here we're crosshatching for 3, the first missing number in this box. Note how we treat the 3 we placed in the first box as if it had been pre-printed on the puzzle. We still can't place this box's 3 though, so we'll move on to the next missing number (5), and so on.

◊ In sudoku, accuracy is essential. If the 3 in the first box is wrong, we'll be starting a chain of errors that may prove impossible to unravel. Only place a number when you can prove, logically, that it belongs there. Never guess, and never follow hunches!

An important factor in crosshatching (and sudoku in general) is that the more numbers you place, the more likely you are to place others - including ones you couldn't place earlier.

Placing numbers in the second box may well make it possible to go back and place missing numbers in the first. It's good to get into the habit of looking backwards as well as forwards, re-checking whether the numbers you've just placed have made numbers placeable elsewhere in the puzzle.

Slicing and dicing

In sudoku it pays to look at the same thing in different ways. By using crosshatching slightly differently, you can often get quicker results.

Instead of looking at a single box and its missing numbers, you can look at a group of three boxes running across or down the puzzle, trying to place each number from 1 to 9 in as many of the boxes as you can.

In this example we're trying to place 7s in the three right-hand boxes:

The stack of boxes starts out with just one 7 in place (bottom box). This solves the middle box's 7 (entered in blue), and entering that immediately solves the top box's 7 as well.

This 'chain reaction' of solving wouldn't occur in single-box crosshatching. It happens here because we're focussing on a single number across multiple boxes - looking at things differently.

Crosshatching and slicing/dicing are basically the same thing, but slicing/dicing can be more efficient, and often feels less laborious than doggedly working through the empty squares in a single box (although that's what you will have to do in order to solve tough puzzles, so be prepared!).

The right start...

It's a good idea to start any puzzle by slicing and dicing, perhaps switching to single-box crosshatching if you get stuck.

Most easy (and many moderate) puzzles can be solved that way - just make a first 'pass' through the whole puzzle placing all the numbers you can, then go back and start again, seeing if any more numbers can now be placed. Keep doing that, and eventually you'll fill the whole puzzle.

In practice you'll soon find that you stop working in passes through the whole puzzle, and begin darting to whichever area looks most likely to have solvable squares.

If you get stuck (i.e. you can't place any more numbers), then it's worth making another methodical pass through the whole puzzle. This will often reveal a solvable square you've missed.

... but when the going gets tough...

On tough puzzles crosshatching and slicing/dicing will eventually run out of steam - you'll make a pass through the whole puzzle without being able to place any more numbers.

When this happens it's time to switch to a different approach, using the solving techniques described in the second part of this page.

The first step, however, is more crosshatching. This time you need to go through the entire puzzle, box by box, crosshatching each box for all its missing numbers. As you do that, you make a note of which squares each missing number can possibly go into. This is called 'pencilling in'.

3. Pencilling in.

The solving techniques needed for more difficult puzzles all depend on having an accurate list of the possible numbers (called 'candidates') for each empty square. You can build this list by pencilling the candidates in as you make a complete crosshatching pass through the puzzle.

Looking at the top-left box of our original puzzle, crosshatching produced three possible squares where the missing 5 could go. Here's the box, with 5 'pencilled-in' to the corners of its three possible squares:

◊ (It's called 'pencilling-in' because on a printed puzzle many people use a pencil, so that they can rub numbers out later (an essential part of the solving process). On my sudoku page, you click in the top-left corner of the square, then type and delete numbers like a normal text box)

1 and 9 were also unsolved for this box. Here's the box with all its missing numbers pencilled into their possible squares:

This list must be complete and accurate, otherwise you risk creating another chain of errors. That's why it's essential to crosshatch every missing number for every box before starting the next stage of solving.

Candidate lists must also be kept up to date (the reasons for this will become obvious later!). Here's what it means:

On the left is is the top-left box, and the one below it. We've just entered a 5 in the bottom-right square of the lower box.

Now we remove that square's candidate list. We also remove 5 from the candidate list at the top of the same column, and the left of the same row. Here's how the boxes look afterwards:

Whenever you fill in a square, remove the number you've used from all candidate lists in the same row, column and box. Here are the areas we needed to check for candidate 5s after filling in this square:

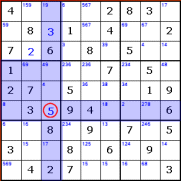
Don't worry if that looks complex - in practice it's quick and easy to scan through the same row, column and box as the square you've just filled.

When you're crosshatching the puzzle, remember to update any candidate lists that are affected by numbers you place.

4. Serious Solving!

It's always worth starting the solving process with a quick slice/dice, because it might solve a square or two even on the toughest puzzle.

However if the puzzle is rated 'hard' or tougher, crosshatching techniques will soon stop producing results. It's best to cut your losses, do the full pencilling-in crosshatch, and move on to some serious solving.

◊ In difficult puzzles with 26 or fewer starting squares, the initial crosshatching run will produce few solved squares, and long lists of candidates. Don't be put off by this - the lists will soon start to shorten as you apply the rules described below.

This part of the solving process is where you switch approach and start finding numbers for squares instead of squares for numbers. You do this by checking your pencilled-in candidate lists for a series of rules (or 'candidate patterns'), and acting on them.

There are lots of rules (and more being discovered all the time), but a basic set of five will solve most puzzles up to 'really tough' or 'fiendish' level. It's worth practicing these until you find yourself recognising the patterns instinctively (it doesn't take long), then adding more rules to your repertoire as they're needed.

Always remember that all rules depend on your candidate lists being complete, accurate and up to date. Get them wrong and you'll soon have big problems!

The first two rules let you solve squares immediately.

Rule 1 - Single-candidate squares.

When a square has just one candidate, that number goes into the square.

Here's the mid-left box again, as it was before we entered the 5:

The mid-right and bottom-right squares each have only one candidate, so we can put those numbers into the squares.

Some squares will be single-candidate from the start of the puzzle. Most, however, will start with multiple candidates and gradually reduce down to single-candidate status.

This will happen as you remove numbers that you've placed in other squares in the same row, column and box, and as you apply the last three rules described below.

Rule 2 - single-square candidates.

When a candidate number appears just once in an area (row, column or box), that number goes into the square.

Look at the mid-left box again:

The number 6 only appears in one square's candidate list within this box (top-middle). This must, therefore, be the right place for the 6.

The remaining three rules let you remove numbers from candidate lists, reducing them down towards meeting one of the first two rules.

Rule 3 - number claiming.

When a candidate number only appears in one row or column of a box, the box 'claims' that number within the entire row or column.

Here's the top-left box again:

The number 1 only appears as a candidate in the top row of the box. This means there will have to be a 1 somewhere in the first three squares of the puzzle's first row (i.e. the ones that overlap with the box). That in turn means that 1 can't go anywhere else in that row, outside of this box.

You can read across the row, and remove 1 from any candidate lists outside of this box, even though you haven't actually placed 1 yet.

In this example, we can remove the 1 from the right-hand square's candidate list. This makes the square single-candidate (7) - square solved!

Claims also work during crosshatching. Here we're crosshatching the top-right box for 1:

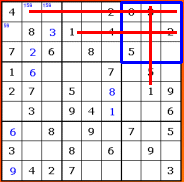
We can rule out the top row, because the top-left box has already claimed that row's 1. This lets us place the 1 in the bottom-right square of the box.

Rule 4 - pairs.

When two squares in the same area (row, column or box) have identical two-number candidate lists, you can remove both numbers from other candidate lists in that area.

Here's the second row of the puzzle:

Two of the squares have the same candidate list - 67. This means that between them, they will use up the 6 and 7 for this row.

That means that the other square can't possibly contain a 6. We can remove the 6 from its candidate list, leaving just 9 - square solved!

The squares in a pair must have exactly two candidates. If one of the above squares had been 679, it couldn't have been part of a pair.

Rule 5 - triples.

Three squares in an area (row, column or box) form a triple when:

None of them has more than three candidates.
Their candidate lists are all full or sub sets of the same three-candidate list (explained below!).

You can remove numbers that appear in the triple from other candidate lists in the same area.

Here's the fourth row of the puzzle:

Note the three squares in the middle, with candidates of 23, 23 and 234. These form a triple.

234 is the full, three-candidate list, and 23 is a subset of it (i.e. all its numbers appear in the full list). Because there are three squares, and none of them have any candidate numbers outside of those in the three-candidate list, they must use up the three candidate numbers (2, 3 and 4) between them.

This lets us remove the 4 from the other two candidate lists in this row, solving their squares.

It's worth looking hard for subset triples. In this example, the 23 lists make an obvious pair (see above), but it's the triple that instantly solves the two outside squares (once you've dispensed with them, you can treat the 23s as a pair again, and use them to solve the 234!). A subset (or 'hidden') triple is often the pattern that will unlock a seemingly impossible puzzle.

Note - the squares in a pair or triple don't have to appear next to each other, or in any particular order. In the example above, the triple could have occurred in, say, the first, third and fifth empty squares of the row, with the 234 in the middle.

Perhaps surprisingly (OK, I was surprised!) the triple rule can be true even if none of the squares have three candidates. Take these three candidate lists:

13 16 36

All three lists are subsets of the list 136. Between them, these three squares will use up the 1, 3 and 6 for the area they're in. These triples can be hard to spot though, so it's probably best to start by looking out for three-candidate squares.

(Special thanks to Edward for pointing out that the members of a triple can all be subsets of the full list!)

◊ If all-subset triples still don't seem right, think of it this way:

The crucial thing is that the number of squares equals the number of candidates in the full list (so three squares all with subsets of '136' (a three-candidate list) makes a triple).

It doesn't matter if some (or all) of the squares don't have the full candidate list. What matters is that between them they cover the list, the whole list and nothing but the list. That means they must use up all three of the list's numbers between them.

In case all that's put you off, here's an example of a more obvious triple - they do exist!:

Pairs and triples are, in fact, variations of the same pattern, sometimes called 'disjoint subsets'. We can express rule 5 in general terms, like this:

A set of N squares in an area forms a group when:

None of the squares has more than N candidates
Their candidate lists are all full or sub sets of the same N-candidate list.

Pairs (N=2) with subset members tend not to survive long, because a subset of a two-number list is a single candidate and thus solvable.

However a single-candidate square can function perfectly well as a member of a pair, or even a triple. This often has the same effect as solving the single-candidate square then updating its surrounding candidate lists, but can be quicker.

On the left is an example (and from an 'easy' rated puzzle, too!)

The top three unsolved squares, with candidates of 26, 23 and 2, form a triple (N=3) with a full list of 236.

That lets us remove the 3 and 6 from the bottom square's candidate list, reducing it to just 8 - square solved!

You also sometimes see 'quadruplets' (N=4) - four squares, none with more than four candidates, and all full or subsets of a four-candidate list.

And, er, that's it....

Using complete, up-to-date candidate lists and the five rules described above, you can solve all but the most extreme sudoku puzzles (using these alone, it's normally possible to solve the 'fiendish' puzzle in the Times newspaper on Fridays).

It's just a matter of scanning through the puzzle, looking for the claim, single-square candidate or triple that will unlock the next stage of the solution.

The harder the puzzle, the harder they tend to be to find, and the fewer 'easy' pairs and single-candidate squares present themselves. But the hard-to-spot rules are in there somewhere - you've just got to find them!

The keys to successful solving are:

Total accuracy - never put a number in a square or candidate list unless you're absolutely sure it's right.
Completeness - make sure to crosshatch every missing number in every box, so that you start the second stage of solving with complete candidate lists.
Maintenance - whenever you place a number in a square, update all the candidate lists in the same row, column and box, straight away (this includes numbers placed during crosshatching).

5. Extreme puzzles.

If the rules described above won't solve a puzzle, then there are two possibilities:

It's a genuinely extreme, but solvable, puzzle, which requires extra rules to solve. In very extreme cases this may involve an element of guesswork (although many people don't regard such puzzles as 'proper' sudoku).
It's not a genuine sudoku puzzle, because it either:

a. Has more than one possible solution, requiring you to make guesses in order to find one of them. (Note that this isn't the same as a single-solution puzzle that requires guesswork - although it may seem pretty similar!)

b. Doesn't have a solution at all.

To check whether a puzzle has more than one solution, type or import it into my page (instructions on page), then press 'Check My Answer'.

Note - if my page gives a puzzle a rating other than 'outlaw', then it's guaranteed to be solvable by logic alone, with no guesses required.

Assuming the puzzle is genuine, a good place to start is with rules 6 and 7 (yes, there are rules 6 and 7!). Here they are:

Rule 6 - excluded candidates.

Within an area (row, column or box), when a set of N candidate lists contain all occurrences of a set of N candidate numbers, other numbers can be removed from those lists.

Note that N is the same both times, so it's three lists containing all occurrences of the same three candidates, and so on.

Here's a (hypothetical) example:

The group comprises squares 1, 2 and 5. All three include the candidates 4, 5 and 7 (three squares, three candidates), and those candidates don't appear in any other lists in this row.

This means that between them, these three squares claim the 4, 5 and 7 for this row. It also means they can't possibly hold any numbers other than 4, 5 or 7.

This lets us remove the other candidate numbers from these squares, like this:

This turns square 6 (18) into the only square with candidate 1, thus solving the square. (Incidentally, there's another way to solve square 6 in this row - can you spot it?)

This rule works with subsets. For example, if the row looked like this:

Square 2's list doesn't contain a 5, but squares 1,2 and 5 still form a valid group. This is because these three squares will still, between them, have to hold the 4, 5 and 7 for this row. Groups like this are just a little bit hard to spot though!

The important thing when looking for this pattern is to make sure none of the candidates appear anywhere else in the area.

Rule 7 - box line reduction.

(Note - I found this rule at Scanraid's excellent solver site).

If all occurrences of a candidate within a row or column fall inside the same box, then other occurrences of that candidate can be removed from that box.

In the right-hand column of this example (not from the sample puzzle), all the occurrences of candidate 1 are in the top box.

This means that the 1 for this box must go in that column, so we can remove 1s from other candidate lists in that box.

This rule is the reverse of rule 3 (number claiming) - instead of the box claiming the number within the row/column, the row/column claims the number within the box.

What if I still can't solve it?

If the puzzle still won't budge, and you're confident that it's valid, then you'll need to enter the exotic world of X Wings, Swordfish and Nishio.

X Wing and Swordfish are patterns that span multiple rows and columns, claiming a candidate number that can then be eliminated from other lists in the relevant columns/rows. They're (fairly) easy to understand but very hard to spot.

Nishio is controversial, as some people regard it as guesswork (you try a number and see if it leads to a dead end) and therefore not proper, logical sudoku solving.

The best explanations I've seen of these patterns are in Simon Armstrong's and Angus Johnson's sudoku solving guides. They describe all the other techniques too, and Simon's was where I discovered the excluded candidates rule. Thanks!

One other (rare) possibility is the remote pair, which is surprisingly simple once you get to grips with it. It's described at http://www.scanraid.com/RemotePairs.htm.

It's worth remembering that spotting these patterns (or using Nishios) is only essential in a small minority of genuinely extreme puzzles. Most puzzles, even 'really tough' and 'fiendish' ones, can be solved by finding every last triple, claim and so on.

Yes, but what about guessing?

Guessing is, in fact, one of the quickest and simplest ways to solve a sudoku - if you're a computer. If you're not, then it's best avoided if at all possible.

Guessing should only be used near the end of a puzzle, when there are 12 or fewer squares left to solve (and preferably 6 or fewer). Any earlier, and it's more likely that either the puzzle is invalid, or you've missed something.

If the puzzle is printed and you've got a photocopier, make a copy (including your solution so far) and work on that. If you're using my page, press 'Save Bookmark' (or export the puzzle as text, copy it to the clipboard and save it via a text editor).

Now find a square with just two candidates (any more and you're asking for trouble!). Choose one of the candidates and pencil it into the square.

The first thing to do is check whether your guess has made the puzzle unsolvable. Update all the candidate lists in the same row, column and box, plus any others that are affected as a result (for example, because a pair or triple has now emerged). Then check the whole puzzle for the following:

A row, column or box from which a number is still missing, but which now doesn't have that number in any of its candidate lists.
A triple which has now become three identical two-candidate squares.
A square which is empty, but now has no candidates.

If any of these occur, then your guess was wrong. Restore your puzzle to its previous state (scrap your copy or press 'restore bookmark'), then try the other candidate as your guess - it should be correct (if it's not, then you've got bigger problems!).

Unfortunately the fact that a guess isn't immediately proved wrong doesn't necessarily mean that it's right. You'll have to go on solving, keeping an eye out for the signs that the puzzle has now become unsolvable.

This is why guessing is best kept to the last stages of the puzzle, where the pathway to either a solution or a dead end is relatively short.

Extra tips - checking that everything's still correct.

Sometimes you might suspect that errors have crept into your candidate lists. One way to check is to re-crosshatch the box where you think the error is, crosshatching for all its missing numbers.

There is, however, another way to check how many candidates a square has. Just read through the row, column and box it belongs to, crossing off all the numbers that appear in them (including any claimed numbers, as long as you're completely sure of them). The numbers that don't appear are that square's candidates.

Here's the whole puzzle, with the row, column and box relevant to the square at row 2, column 1 highlighted:

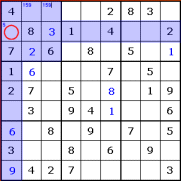
Check off the numbers that already appear in these areas, and you'll find the list reads 1,2,3,4,6,7,8,9 - only 5 is missing.

This technique (like crosshatching) will only restore the starting value of a candidates list, not any reductions you'd found by applying the rules described above.

Errors in candidate lists are relatively easy to deal with. Errors in placed numbers are much more dangerous, because they can corrupt all the candidate-list calculations around them. Always double (or triple) check that a number is right before placing it as a square's value. If you want to avoid serious headaches, never guess!

6. Quick Solving Checklist

Here's a quick checklist of the solving plan for tough puzzles.

1. Try slicing and dicing to solve any easy squares. Don't spend too long on it though.

2. Crosshatch the entire puzzle box-by-box, pencilling-in complete candidate lists.

3. Scan the puzzle for the following rules:

Single-candidate squares - solve immediately
Single-square candidates within an area (row/column/box) - solve immediately.
Claims by a box - remove the claimed candidate from the same row/column in other boxes.
Pairs within an area - remove the pair squares' candidates from other lists within that area.
Triples within an area - remove the triple candidates from others lists within that area.

4. Whenever you solve a square, immediately check and update all candidate lists in the same row, column and box.

5. Whenever you've updated a candidate list, check to see if one of the rules now applies (e.g. you've created a triple, or a box is now claiming a number).

6. Never guess! (Unless you're absolutely sure you have to!)

Have fun!

Paul Stephens, June 2005.